Découvrez en détail la notation Grand O (a.k.a Big O) et explorez les subtilités de la performance et de la complexité temporelle en algorithmique à travers des exemples concrets en Python. Maîtrisez l'art de concevoir des algorithmes performants.
Dans le vaste domaine de la programmation, la quête de l’efficacité est une constante. Choisir le bon algorithme peut faire la différence entre un code qui s’exécute avec agilité et un code qui peine sous la pression. C’est là qu’intervient la notation du “Grand O”, un outil essentiel pour évaluer et comparer les performances des algorithmes.
Pour ceux d’entre nous qui ont façonné des lignes de code pendant des années, la complexité algorithmique est bien plus qu’une simple notation mathématique. C’est une clé pour comprendre comment nos choix de conception affectent la vitesse et la scalabilité de nos applications. C’est le langage des experts, celui qui distingue ceux qui écrivent du code de ceux qui conçoivent des systèmes robustes.
Dans cet article, nous allons plonger dans les tréfonds de différentes notations du Grand O. À travers des exemples pratiques en Python, nous allons explorer comment des algorithmes, même en apparence similaires, peuvent avoir des performances radicalement différentes. Nous allons disséquer des itérations et des récursions, évaluer des tris et des recherches, et nous imprégner du sens profond de ces notations.
Que vous soyez un codeur chevronné ou un passionné qui cherche à maîtriser les subtilités de la complexité algorithmique, ce guide vous offrira un aperçu de pointe sur la notation Grand O et son impact sur la construction de systèmes informatiques robustes.
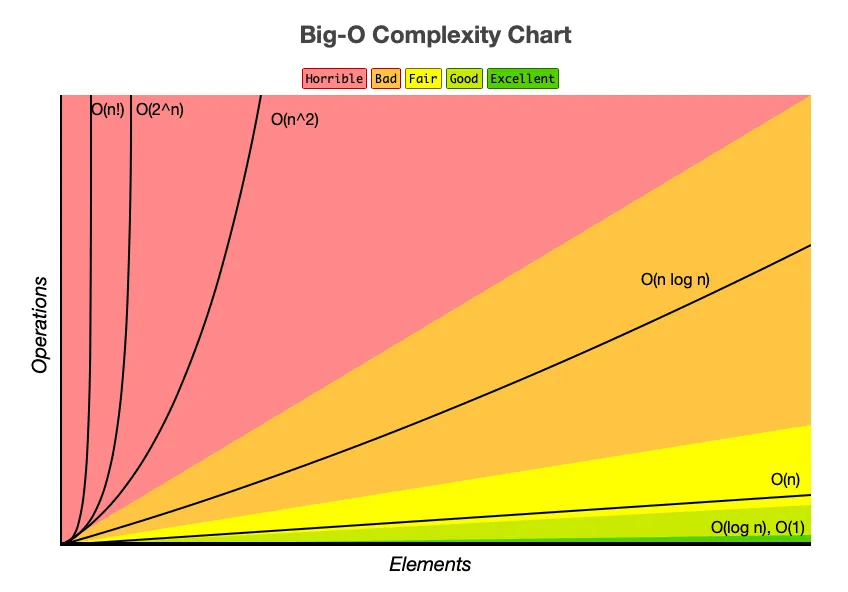
Gardez bien ce graphique ci-dessus en tête tout le long de l’article. Il permet de donner une idée rapide des complexités temporelles (a.k.a Complexité en temps) que nous allons aborder.
Complexité des algorithmes
Il existe deux types de complexité pour mesurer la performance d’un algorithme :
- complexité spatiale : quantifie l’utilisation de la mémoire.
- complexité temporelle : quantifie la vitesse d’exécution.
Et c’est de cette dernière que nous allons parler.
La complexité en temps d’un algorithme est un concept fondamental qui mesure la quantité de temps nécessaire pour exécuter un algorithme en fonction de la taille de l’entrée. Elle permet d’évaluer les performances d’un algorithme et de prédire comment celles-ci évolueront lorsque la taille des données augmente.
Complexité O(1) - Complexité constante
La complexité O(1), également connue sous le nom de complexité constante, représente l’idéal de l’efficacité algorithmique. Elle signifie que le temps d’exécution de l’algorithme reste constant, quelle que soit la taille de l’entrée. Peu importe si la liste contient 10 éléments ou 10 000, l’algorithme effectuera le même nombre d’opérations.
Illustration avec un accès à un élément dans un tableau
Un exemple concret de la complexité O(1) est l’accès à un élément dans un tableau par son index. Peu importe la taille du tableau, l’accès à un élément spécifique se fait en temps constant.
def access_element(arr, index):
return arr[index]
Dans cette fonction, arr est le tableau et index est l’indice de l’élément que nous voulons accéder. L’opération d’accès à l’élément ne dépend pas de la taille du tableau, ce qui en fait un exemple classique de complexité constante.
Mesure de la performance en temps d’exécution
Lorsque nous mesurons le temps d’exécution de cet algorithme avec des tableaux de différentes tailles, nous constaterons que le temps reste essentiellement le même, quel que soit le nombre d’éléments dans le tableau.
import time
# Exemple de la complexité O(1)
def access_element(arr, index):
return arr[index]
arr = list(range(1000000)) # Une grande liste pour illustrer
target = 500000
start_time = time.time()
access_element(arr, target)
print(f"Temps pour O(1) : {time.time() - start_time} secondes")
Analyses et cas d’utilisation
La complexité O(1) est la pierre angulaire de l’efficacité algorithmique. Elle est souvent utilisée dans des opérations fondamentales telles que l’accès à des éléments dans des structures de données, l’ajout et la suppression d’éléments à la fin d’une liste, et bien d’autres. Les algorithmes qui maintiennent une complexité constante sont considérés comme extrêmement performants et sont la base de nombreuses opérations courantes en programmation.
Complexité O(log n) - Complexité logarithmique
La complexité O(log n), souvent appelée complexité logarithmique, est une pierre angulaire de l’efficacité algorithmique. Elle représente un équilibre entre performances élevées et des données de taille considérable. Cette complexité se trouve fréquemment dans des algorithmes qui divisent le problème en parties plus petites à chaque itération.
Exemple de la complexité O(log n) avec la recherche binaire
Un exemple emblématique de complexité logarithmique est la recherche binaire. Dans cette méthode, une liste triée est divisée en deux à chaque itération, réduisant ainsi le champ de recherche de moitié à chaque étape.
def binary_search(arr, target):
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1
L’efficacité de la recherche binaire provient de sa capacité à éliminer une grande partie de l’espace de recherche à chaque itération, ce qui conduit à une croissance logarithmique du temps d’exécution.
Analyse des avantages de cette complexité
Bien que la complexité logarithmique soit extrêmement efficace, elle n’est pas toujours une solution miracle. Elle trouve sa force dans des domaines spécifiques où les données peuvent être divisées de manière significative. Cependant, elle peut être moins performante lorsque les données ne peuvent pas être rapidement réduites. Il est essentiel de comprendre les caractéristiques de chaque problème pour choisir l’approche algorithmique la plus adaptée.
Comparaison avec des complexités linéaires
Comparée à une complexité linéaire (O(n)), où le temps d’exécution augmente proportionnellement à la taille des données, la complexité logarithmique offre des performances nettement supérieures pour les ensembles de données volumineux.
Complexité O(n) - Complexité linéaire
La complexité O(n), également connue sous le nom de complexité linéaire, est un concept fondamental en algorithmique. Elle indique que le temps d’exécution d’un algorithme est proportionnel à la taille de l’entrée. En d’autres termes, à mesure que la taille des données augmente, le temps nécessaire pour traiter ces données augmente linéairement.
Illustration avec la recherche séquentielle
Un exemple concret de la complexité O(n) est la recherche séquentielle dans une liste non triée. L’algorithme parcourt chaque élément de la liste jusqu’à ce qu’il trouve la cible ou atteigne la fin de la liste.
def find_element(arr, target):
for elem in arr:
if elem == target:
return True
return False
Dans cet exemple, arr est la liste d’éléments et target est l’élément que nous voulons trouver. Le temps nécessaire pour trouver l’élément dépend directement de la taille de la liste.
Analyse et mesure de la performance en temps d’exécution
Lorsque nous mesurons le temps d’exécution de cet algorithme avec des listes de différentes tailles, nous observons une croissance linéaire du temps d’exécution. Plus la liste est longue, plus le temps nécessaire pour trouver l’élément peut être important.
La complexité linéaire est une amélioration significative par rapport à des complexités plus élevées, mais elle présente ses propres limites. Lorsque les ensembles de données sont très volumineux, même une complexité linéaire peut entraîner des temps d’exécution indésirables. Dans de tels cas, il peut être nécessaire d’explorer des algorithmes plus sophistiqués avec des complexités inférieures pour garantir des performances optimales.
Situations où O(n) est incontournable
La complexité linéaire est souvent inévitable dans de nombreuses situations. Par exemple, lorsque les données ne sont pas triées et que la recherche d’un élément spécifique est nécessaire, la recherche séquentielle (complexité O(n)) est la méthode appropriée. De plus, de nombreuses opérations qui nécessitent de parcourir l’ensemble des données, telles que la somme de tous les éléments d’une liste, ont une complexité linéaire.
Complexité O(n log n) - Complexité n log n
La complexité O(n log n) est une classe de complexité particulièrement intéressante et courante. Elle se situe entre la complexité linéaire et la complexité quadratique, offrant un équilibre entre performances élevées et la capacité à traiter des ensembles de données de taille considérable.
Exemple avec le tri fusion
Un exemple représentatif de la complexité O(n log n) est l’algorithme de tri fusion. Cette méthode de tri divise la liste en deux moitiés, trie récursivement chaque moitié, puis fusionne les résultats triés.
def merge_sort(arr):
if len(arr) <= 1:
return arr
mid = len(arr) // 2
left = arr[:mid]
right = arr[mid:]
left = merge_sort(left)
right = merge_sort(right)
return merge(left, right)
def merge(left, right):
result = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result.extend(left[i:])
result.extend(right[j:])
return result
Le tri fusion illustre la puissance de la complexité O(n log n) en exploitant la nature diviser-pour-régner pour trier efficacement de grandes quantités de données.
Comparaison avec des complexités quadratiques
Comparée à une complexité quadratique (O(n²)), qui peut devenir prohibitivement lente pour de grandes quantités de données, la complexité O(n log n) offre une amélioration significative des performances, ce qui en fait un choix populaire pour de nombreuses applications.
Cas d’utilisation et efficacité
La complexité O(n log n) est couramment utilisée dans une variété d’algorithmes de tri (comme le tri rapide) et d’autres algorithmes de traitement de données qui exploitent la méthode diviser-pour-régner. Elle est également fondamentale dans des domaines tels que la conception d’algorithmes d’optimisation et la recherche d’arbres binaires équilibrés.
Dans des cas où les données sont déjà triées ou presque triées, il peut être plus avantageux d’utiliser des algorithmes avec des complexités linéaires. De plus, pour de très petites tailles de données, la complexité n log n peut avoir une constante multiplicative plus élevée que d’autres algorithmes, ce qui la rend moins efficace dans ces cas.
Complexité O(n²) - Complexité quadratique
La complexité O(n²) est un scénario à éviter lorsque cela est possible. Elle indique que le temps d’exécution d’un algorithme augmente quadratiquement avec la taille de l’entrée. En d’autres termes, lorsque la taille des données double, le temps d’exécution peut quadrupler.
Exemple avec le tri à bulles
Un exemple emblématique de complexité O(n²) est l’algorithme de tri à bulles. Dans cet algorithme, les éléments adjacents de la liste sont comparés et échangés s’ils sont dans le mauvais ordre. Ce processus est répété jusqu’à ce que la liste soit triée.
def bubble_sort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
return arr
S’il s’agissait d’un algorithme O(n), nous effectuerions un total de 3 itérations, puisque la liste comporte 3 éléments. Mais avec les boucles imbriquées, nous finissons par effectuer 9 itérations. C’est pourquoi la complexité temporelle est polynomiale, O(n^2), car 3^2 = 9.
Le tri à bulles est simple à implémenter, mais il est inefficace pour de grandes quantités de données en raison de sa complexité quadratique.
Analyse des inconvénients de la complexité O(n²)
La complexité quadratique peut rapidement devenir problématique pour des ensembles de données volumineux. À mesure que la taille des données augmente, le temps nécessaire pour effectuer les opérations peut croître de manière exponentielle, ce qui peut conduire à des temps d’exécution inacceptables.
Alternatives pour optimiser les performances de O(n²)
Face à une complexité quadratique, il est souvent judicieux d’explorer des algorithmes plus efficaces avec des complexités inférieures, comme les algorithmes de tri avec une complexité O(n log n), tels que le tri rapide ou le tri fusion.
Complexité O(2ⁿ) - Complexité exponentielle
La complexité O(2ⁿ), souvent qualifiée de complexité exponentielle, représente l’un des pires scénarios en termes d’efficacité algorithmique. Elle indique que le temps d’exécution de l’algorithme double (ou augmente de manière exponentielle) avec chaque augmentation de la taille de l’entrée.
Exemple avec la suite de Fibonacci inefficace
Un exemple classique de complexité exponentielle est le calcul de la suite de Fibonacci de manière récursive inefficace. Dans cette approche, le calcul de chaque terme de la suite dépend de deux appels récursifs.
def fib(n):
if n <= 1:
return n
return fib(n-1) + fib(n-2)
Bien que cette méthode calcule correctement la suite de Fibonacci, elle devient rapidement inefficace pour des valeurs de n relativement modestes, car elle effectue de nombreuses redondances de calcul.
Par ailleurs,
Si vous souhaitez essayer un algorithme avec une complexité O(2ⁿ) :
import time
# Choisir une valeur appropriée pour n
n = 20
start_time = time.time()
result = fib(n)
print(f"Fibonacci de {n} : {result}")
print(f"Temps pour O(2ⁿ) : {time.time() - start_time} secondes")
Limites et défis de cette complexité
La complexité exponentielle est synonyme de défis colossaux en termes de performance. Pour des ensembles de données de taille modeste, cela peut être gérable, mais dès que la taille des données augmente, le temps d’exécution peut devenir prohibitif. Face à une complexité exponentielle, il est impératif de rechercher des algorithmes plus efficaces ou d’exploiter des propriétés spécifiques du problème pour obtenir des résultats acceptables dans un délai raisonnable.
Recherche de solutions alternatives
Face à une complexité exponentielle, il est impératif de rechercher des algorithmes plus efficaces. Dans le cas de la suite de Fibonacci, par exemple, des approches itératives ou des méthodes exploitant des propriétés mathématiques spécifiques peuvent fournir des résultats beaucoup plus rapidement.
Complexité O(n!) - Complexité factorielle
La complexité O(n!), également connue sous le nom de complexité factorielle, représente l’un des pires scénarios en termes d’efficacité algorithmique. Elle indique que le temps d’exécution de l’algorithme augmente de manière astronomique avec chaque augmentation de la taille de l’entrée.
Exemple avec le problème du voyageur de commerce
Un exemple emblématique de complexité factorielle est le problème du voyageur de commerce. Dans ce casse-tête, il s’agit de déterminer le chemin le plus court qui passe par toutes les villes, en visitant chaque ville exactement une fois et en retournant à la ville d’origine.
import itertools
import time
def calculate_total_distance(path, distances):
total_distance = 0
for i in range(len(path) - 1):
total_distance += distances[path[i]][path[i+1]]
total_distance += distances[path[-1]][path[0]]
return total_distance
def traveling_salesman_bruteforce(distances):
num_cities = len(distances)
all_cities = set(range(num_cities))
shortest_path = None
shortest_distance = float('inf')
for path in itertools.permutations(all_cities):
total_distance = calculate_total_distance(path, distances)
if total_distance < shortest_distance:
shortest_distance = total_distance
shortest_path = path
return shortest_path, shortest_distance
# Création d'une matrice de distances entre les villes (à titre d'exemple)
distances = [[0, 10, 15, 20],
[10, 0, 35, 25],
[15, 35, 0, 30],
[20, 25, 30, 0]]
start_time = time.time()
path, distance = traveling_salesman_bruteforce(distances)
print(f"Chemin le plus court : {path}, Distance : {distance}")
print(f"Temps pour O(n!) : {time.time() - start_time} secondes")
Dans cet exemple, l’algorithme explore toutes les permutations possibles pour trouver le chemin le plus court. Pour un grand nombre de villes, le nombre de permutations augmente de façon astronomique, ce qui rend cette approche impraticable.
Analyse des limitations et défis
La complexité factorielle est souvent un signal d’alarme clair quant à l’efficacité d’un algorithme. Avec une croissance de l’ordre de n!, même des ensembles de données relativement petits peuvent provoquer des temps d’exécution extrêmement longs. Dans de tels cas, il est essentiel d’explorer des alternatives plus efficaces ou de revoir la formulation du problème pour éviter des coûts prohibitifs en termes de temps de calcul. Cette complexité requiert souvent des techniques d’optimisation créatives et la recherche d’approches algorithmiques plus adaptées.
Recherche de solutions alternatives
Face à une complexité factorielle, il est crucial d’explorer des approches plus intelligentes ou des heuristiques qui peuvent fournir des résultats acceptables dans des délais raisonnables. Dans le cas du voyageur de commerce, des algorithmes d’approximation tels que l’algorithme de l’arbre couvrant minimum peuvent être utilisés pour trouver des solutions proches de l’optimal.
Perspectives avancées, complexité “exotique”
Au-delà des notations du Grand O couramment rencontrées, il existe des complexités algorithmiques plus spécifiques et parfois surprenantes qui peuvent se présenter dans des domaines spécialisés de la programmation. Voici quelques-unes de ces perspectives avancées :
- O(sqrt(n)) - Complexité Racine Carrée : Cette complexité se trouve parfois dans des algorithmes d’exploration de graphes comme l’algorithme de recherche en largeur (BFS) sur certains types de graphes particuliers.
- O(n log log n) - Complexité n Log Log N : Cette complexité apparaît dans des algorithmes avancés de manipulation de données, tels que l’algorithme de criblage d’Ératosthène pour la recherche de nombres premiers.
- O(poly(n)) - Complexité Polynomiale : Alors que les complexités exponentielles sont souvent redoutées, les complexités polynomiales (comme O(n^2) ou O(n^3)) peuvent être tout à fait acceptables pour des ensembles de données de taille modérée.
- O(n^c), c > 1 - Complexité Polynomiale Supérieure : Ces complexités sont plus coûteuses que les polynômes de degré inférieur, mais moins coûteuses que les exponentielles. Elles sont souvent associées à des algorithmes d’optimisation.
- O(n^log(n)) - Complexité Quasi-Linéaire : Cette complexité est rare mais peut se présenter dans des algorithmes de manipulation de données complexes tels que l’algorithme de transformation de Fourier rapide (FFT).
Il est important de noter que ces complexités ne sont pas aussi courantes que les exemples précédemment discutés, et elles sont généralement spécifiques à des domaines d’application très spécialisés. Cependant, elles démontrent la diversité des performances algorithmiques et soulignent l’importance de choisir des algorithmes adaptés à des problèmes spécifiques. Lorsqu’on se trouve face à des problèmes complexes, il est souvent utile de consulter la littérature spécialisée et de considérer des approches algorithmiques moins conventionnelles pour trouver des solutions optimales.
Le chemin de l’apprentissage et de la maîtrise de la programmation peut parfois être ardu, avec ses défis et ses moments de frustration. Mais n’oubliez jamais que chaque obstacle est une opportunité d’apprendre et de grandir. Chaque ligne de code qui ne fonctionne pas comme prévu est une invitation à trouver une solution plus élégante et efficace.